Space Syntax for Dummies | Part 2
BASICS
by Dr. Mark David Major, AICP, CNU-A, The Outlaw Urbanist contributor

Continuing our three-part series on the basics of space syntax, Part 2 is based on excerpts from Chapter 3 of my forthcoming Relentless Magnificence: The American Urban Grid. As such, it is somewhat tailored to an American audience. The key principles discussed here are representation and configuration. What is configuration? In the simplest terms, using the most convenient definitions, configuration is not how one thing relates to another thing but how that one thing relates to all other things and also how all those other things relate to each other.

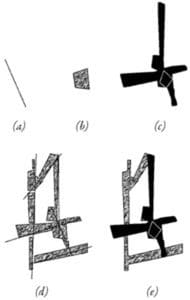
According to space syntax theory, a key to understanding urban space is a description not just of the individual elements in the city (this street or that square) but a description of the entire spatial system considered as a configurational network. Over the last three decades, spaces syntax research programs around the world have developed a series of representational and analytical techniques based on simple descriptions of space (Hillier and Hanson, 1984; Hillier, 1996; Hanson, 1998). By simple description, we mean representations that obey real physical constraints the built environment places on visibility and movement since you cannot see and move through solid objects but only through open and accessible space. First, the movement of a person or persons through the built environment tends to be linear so one representation used is the axial line or axis (see ‘a’ above). The matrix of the longest and fewest lines of sight and access that completely encompasses all the spaces of a built environment is the axial map. Second, previous research has found the occupation of space by people in the built environment will tend towards convexity, the mathematical definition of all points being visible to all others, such as a group of people gathered in a circle (Hillier et al, 1996; Campos, 1997). This simple description is a convex space (see ‘b’ above). The collection of the fattest two-dimensional lumps of space, or convex spaces, in a built environment is the convex map. Finally, the potential for seeing and moving in the built environment can also form the basis for a simple description of space, which Benedikt (1990) called the isovist or, more simply, the visual field at eye level (see ‘c’ above) (Hillier et al, 1987; Conroy Dalton et al, 2003). An isovist describes all visible and accessible space to which a person or persons might move as defined from a particular point or set of points. Later methodological developments in space syntax allow for the measurement of the configurational relationship of all visual fields from a gridded set of points (or point isovists) to all others in a built environment. These form a matrix of visual fields where some are more strategic than others for understanding the spatial network as a whole (see the space syntax model of visual fields in the Tate Gallery, Millbank in Space Syntax for Dummies, Part 1). This is a visibility graph (Turner and Penn, 1999). Finally, any combination of these representations can be used to create a more complex picture of the built environment, depending on the problem researched (see ‘d-e’ above). Hillier (2005) describes these simple descriptions as “a natural and necessary spatial geometry (which) describes some aspect of how buildings and cities are organized… as a vital aspect of how we create them, use them and understand them” (5). This is how to represent space.

However, some additional clarification is required about what is meant by configuration. Configuration is a relational system based on topological graph theory whereby any local changes in that system can have global effects across that system (Hillier, 1993; Hillier, 1996).

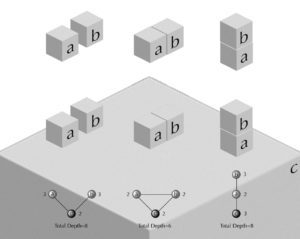
For example, two objects are in a mathematical relationship to each other so it can be said that ‘a’ is to ‘b’ as ‘b’ is to ‘a’ (see above, top). Once this relationship is established with reference to a third object, in this case the surface of the earth, there is a configurational relationship (see above, bottom). If the objects are distinct, then it can be said ‘a’ is to ‘c’ as ‘b’ is to ‘c’ but, in order to reach ‘a’ from ‘b’ or vice versa, one has to pass through ‘c’. This can be seen more clearly in the corresponding topological graph where ‘c’ is shallower to ‘a’ and ‘b’ than they are to each other. The depth of ‘a’ or ‘b’ to any other object in the system is three whereas the depth from ‘c’ to ‘a’ or ‘b’ is two and total depth in the system of objects is eight. Next, ‘a’ and ‘b’ can be placed next to each other to introduce the idea of permeability or connection into the system of objects. The objects are in a symmetrical relationship where all spaces are maximally shallow from each other, so that ‘a’ is to ‘b’ as ‘b’ is to ‘c.’ In this case, the depth from any object to any other is two and total depth in the system is six. Finally, if ‘b’ is placed on top of ‘a’, this forms an asymmetrical relationship with reference to ‘c.’ You have to pass through ‘a’ in order to reach ‘b’ from ‘c’ or vice versa but you are not required to pass through ‘b’ to go from ‘c’ to ‘a.’ In this case, the depth of ‘b’ and ‘c’ is three and depth from ‘a’ is only two. Total depth in this asymmetrical relationship is eight (Major, 2000). According to Hillier (2005), “space syntax seeks to formulate mathematically the configurational properties of space that we intuit, as manifested in the way… we construct real spatial patterns through building and cities” using topological graph theory to objectively measure these spatial patterns (6).

These are the basic principles underlying space syntax.

Additional Reading and References
For your convenience, the easiest reading below is indicated with an *asterisk.

Benedikt, Michael L. 1979. “To take hold of space: Isovists and Isovists Fields”, Environment and Planning B: Planning and Design, 6: 47-66. Article is currently available online for download from the Massachusetts Institute of Technology here.

Campos, Maria Beatriz de Arruda. 1997. “Strategic Space: Patterns of Use in Public Square of the City of London”, First International Space Syntax Symposium Proceedings (Eds. M.D. Major, L. Amorim, F. Dufaux), 2: 26.1-26.11. Article is currently available online for download via the Space Syntax Network here.

Conroy Dalton, Ruth and S. Bafna. 2003. “The syntactical image of the city: A reciprocal definition of spatial elements and spatial syntaxes”, Fourth International Space Syntax Symposium Proceedings, London, 2003: 59.1-59.22. Article is currently available online for download via the Space Syntax Network here.

Hanson, Julienne. 1998. Decoding Homes and Houses. Cambridge: Cambridge University Press. Available for purchase from Amazon here.

Hillier Bill. 2005. “The art of place and the science of space”, World Architecture, Special Issue on Space Syntax. Beijing: 11(185): 24-34 (in Chinese); 96-102 (in English). Article is currently available online for download from Scribd here. Registration required.

*Hillier, Bill. 1996. Space is the Machine: A Configurational Theory of Architecture. Cambridge: Cambridge University Press. Digital eBook is available for free download from University College London here.

*Hillier, Bill, M.D. Major, J. Desyllas, K. Karimi, B. Campos, T. Stonor. 1996. Tate Gallery, Millbank: A Study of the Existing Layout and New Masterplan Proposal. Technical Report, Unit For Architectural Studies, Bartlett School of Graduate Studies, University College London. Report is available for free download from University College London here.

*Hiller, Bill, J. Hanson, H. Graham. 1987. “Ideas are in things: an application of space syntax method to discovering housing genotypes”, Environment and Planning D: Planning and Design, 14: 363-385. Article is available for free download from University College London here.

Hillier, Bill and J. Hanson. 1984. The Social Logic of Space. Cambridge: Cambridge University Press. Available for purchase from Amazon here.

*Major, M.D. 2014. Relentless Magnificence: The American Urban Grid. Jacksonville, Florida: Forum Books, forthcoming.

Turner, Alasdair and A. Penn. 1999. “Making Isovists Syntactic: isovist integration analysis”, Second International Space Syntax Symposium Proceedings (Eds. F. de Holanda, L. Amorim, F. Dufaux), 1:11.01-11.14. Article is currently available online for download via the Space Syntax Network here.

Stay tuned for Space Syntax for Dummies, Part 3: Results.